This page provides topic-wise solved past papers under the chapter Number for the IGCSE Mathematics 0580 syllabus. Each question is solved in detail, allowing you to understand the reasoning and steps in reaching the correct answer. While the solutions are thorough to aid your learning, it’s important to note that you won’t need to solve in such detail during the exam itself. The step-by-step approach enhances your understanding, making it easier to apply more concise methods when answering questions under timed conditions.
1.1 Types of Number
0580/12/02/03/24/01
Write the number thirty thousand and fifty in figures.
Answer is 30,050
1.4 Fractions, decimals, and percentages
0580/12/02/03/24/08
Calculate $\quad \sqrt{5.76} + 2.8^3$
Calculate the square root of 5.76 $\quad\quad \sqrt{5.76} = 2.4$
Calculate the cube of 2.8 $\quad\quad\quad 2.8^3 = 2.8 \times 2.8 \times 2.8 = 21.952$
Add the two results $\quad\quad\quad\quad\quad 2.4 + 21.952 = 24.352$
Answer is 24.352
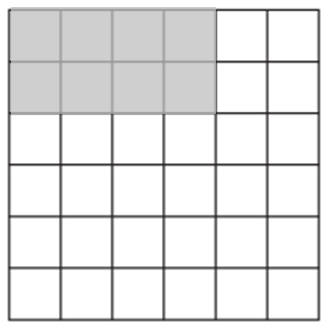
0580/12/02/03/24/04a
Shade $\frac{2}{9}$ of this shape.

Determine the total number of squares
The shape is a grid made up of smaller squares. Count the total number of small squares in the grid. From the image, there are 6 rows and 6 columns:
$$ 6 \times 6 = 36 \text{ squares} $$
Calculate $\frac{2}{9}$ of the total number of squares
To find how many squares correspond to $\frac{2}{9}$ of the total grid, multiply the total number of squares by $\frac{2}{9}$:
$$\frac{2}{9} \times 36 = 8$$
Shade 8 squares
Shade 8 squares out of the total 36 squares. If they add up to the correct fraction, you can choose any 8 squares in the grid to shade.
0580/12/02/03/24/04b
Write $\frac{2}{9}$ as a percentage.
Divide the numerator by the denominator to convert it to a decimal:
$$ \frac{2}{9} = 0.\overline{2} \quad\text{(repeating decimal)} $$
This is approximately $0.222$ when rounded to three decimal places.
Multiply the decimal by 100 to convert it to a percentage:
$$ 0.222 \times 100 = 22.2\% $$
Answer is $22.2\%$
0580/12/02/03/24/24
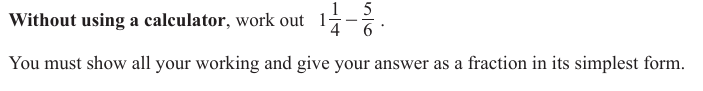
Convert the mixed number into an improper fraction.
The mixed number $1 \frac{1}{4}$ is converted as follows: $\quad\quad1 \frac{1}{4} = \frac{5}{4}$
Next, subtract the fractions. $\quad\quad\frac{5}{4} – \frac{5}{6}$
To subtract these, we need to find a common denominator. The least common denominator (LCD) of 4 and 6 is 12.
Convert the fractions to have the same denominator.
- Convert $\frac{5}{4}$ to have a denominator of 12: $\quad\quad\frac{5}{4} = \frac{15}{12}$
- Convert $\frac{5}{6}$ to have a denominator of 12: $\quad\quad\frac{5}{6} = \frac{10}{12}$
Now, subtract the two fractions.$\quad\quad\frac{15}{12} – \frac{10}{12} = \frac{5}{12}$
Answer is $\frac{5}{12}$.
1.8 Standard Form
0580/12/02/03/24/22
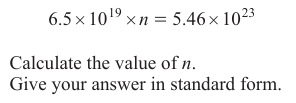
First isolate $n$ by dividing both sides of the equation by $6.5 \times 10^{19}$
$$n = \frac{5.46 \times 10^{23}}{6.5 \times 10^{19}}$$
Divide the coefficients:
$$\frac{5.46}{6.5} \approx 0.84$$
Then subtract the exponents:
$$10^{23} \div 10^{19} = 10^{23 – 19} = 10^{4}$$
Then, combine the results:
$$n = 0.84 \times 10^{4}$$
Finally, express in standard form:
$$n = 8.4 \times 10^{3}$$
Answer is $8.4 \times 10^{3}$
1.9 Estimation & Approximations
0580/12/02/03/24/02
Write 5926 correct to the nearest 10.
To round 5926 to the nearest 10:
- Look at the unit digit, which is 6.
- Since the unit digit is 5 or greater, round up the tens digit.
So, 5926 rounded to the nearest 10 is 5930.
1.10 Limits of Accuracy
0580/12/02/03/24/21

Find the lower-bound
The smallest possible value of 𝑙 would be when it rounds up to 18.7 meters. This would be halfway between 18.6 and 18.7 meters:
Lower bound = $18.7 − 0.05$ = $18.65$ m
Find the upper-bound
The largest possible value of 𝑙 would be just below the next 10-centimeter increment, which is 18.8 meters:
Upper bound = $18.7 + 0.05$ = $18.75$ m
So, the length 𝑙 lies between 18.65 m and 18.75 m. Therefore, the inequality is:
$$
18.65 \leq l < 18.75
$$
1.15 Time
0580/12/02/03/24/05
A night bus runs from 21 50 to 05 18 the next day.
Work out the number of hours and minutes that the night bus runs.
- Start time: 21:50
- End time: 05:18 the next day
Calculate the time from 21:50 to 00:00 (midnight):
- From 21:50 to 22:50 is 1 hour.
- From 22:50 to 00:00 is 1 hour and 10 minutes.
- Total time before midnight: 2 hours and 10 minutes.
Calculate the time from 00:00 to 05:18:
- From 00:00 to 05:18, it is 5 hours and 18 minutes.
Add the two-time intervals
- Before midnight: 2 hours and 10 minutes
- After midnight: 5 hours and 18 minutes
Add hours and minutes together:
- Hours: 2 + 5 = 7 hours
- Minutes: 10 + 18 = 28 minutes
Answer is 7 hours and 28 minutes
1.16 Money
0580/12/02/03/24/16

Convert rupees into dollars
The total amount in rupees is 17,850. Since 1 rupee equals 0.013 dollars, we can calculate how many dollars this is:
$$
\text{Dollars} = \frac{17850}{1} \times 0.013 = 232.05 \, \text{dollars}
$$
Convert dollars into euros
Since 1 euro equals 1.05 dollars, we can calculate how many euros were used to get those 232.05 dollars:
$$
1 \, \text{euro} = 1.05 \, \text{dollars}
$$
So,
$$
x = \frac{232.05}{1.05} \approx 221 \, \text{euros}
$$
Answer is 221
1.19 Factors, Multiples, and Divisibility
0580/12/02/03/24/06a
$$34\quad 55\quad 76\quad 83\quad 111\quad 121$$
From this list of numbers, write down all the multiples of 11.
Check for multiples of 11:
55: $\frac{55}{11}$ = 5 (Exactly divisible by 11)
121: $\frac{121}{11}$ = 11 (Exactly divisible by 11)
34, 76, 83, and 111 are not exactly divisible by 11.
Answer is 55, 121
0580/12/02/03/24/06b
Zaid has a non-calculator method for working out if a number is a multiple of 11.
He shows his method for the number 919281.
Subtract and add alternately the digits in the number. 9-1+9-2+8-1=22
Check if the answer is a multiple of 11. 22 = 2 x 11
As 22 is a multiple of 11 then 919281 is a multiple of 11.
Show that the number 918271937 is a multiple of 11 by using Zaid’s method.
Write down the number and alternate between subtracting and adding its digits:
$$9−1+8−2+7−1+9−3+7$$
Calculate the alternating sum:
$$9−1=8$$
$$8+8=16$$
$$16−2=14$$
$$14+7=21$$
$$21−1=20$$
$$20+9=29$$
$$29−3=26$$
$$26+7=33$$
The final result is 33, which is a multiple of 11.
$$\frac{33}{11} = 3$$
33 is exactly divisible by 11. Hence, 918271937 is also a multiple of 11.
0580/12/02/03/24/10a
$$-9\quad\quad -7\quad\quad -3\quad\quad -1\quad\quad 0\quad\quad 2\quad\quad 5\quad\quad 6\quad\quad 8$$
From this list of numbers, find
The highest number possible from the product of two of the numbers.
Consider the two largest positive numbers which are 6 and 8. $\quad 6\times 8 = 48$
Multiplying two negative numbers will give a positive result.
Consider the two largest negative numbers, which are -7 and -9. $\quad -7\times -9 = 63$
The highest number possible from the product of two numbers is 63.
0580/12/02/03/24/10b
The lowest number possible from the product of three of the numbers.
Given numbers: $\quad -9,-7,-3,-1,0,2,5,6,8$
Choose one largest negative number and two largest positive numbers $\quad -9,6,8$
Multiply them: $\quad\quad -9\times 6\times 8 = -432$
Answer -432
0580/12/02/03/24/25

We know that
HCF x LCM = Product of the two numbers
Substituting the given values:
6 x 90 = Product of the two numbers
Product of the two numbers = 540
Next, we find two numbers whose HCF is 6 and product is 540.
Let the two numbers be 6$a$ and 6$b$.
6$a$ x 6$b$ = 540
36$ab$ = 540
$ab$ = 15
Now, find the co-prime numbers whose product is 15:
$a$ = 3, and $b$ = 5
Multiply both $a$ and $b$ by 6 to find the original numbers:
6$a$ = 6 x 3 = 18
6$b$ = 6 x 5 = 30
The two numbers are 18 and 30.