Number

0580/12/02/03/24/03

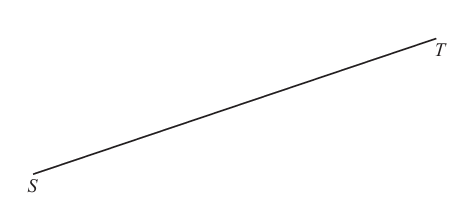
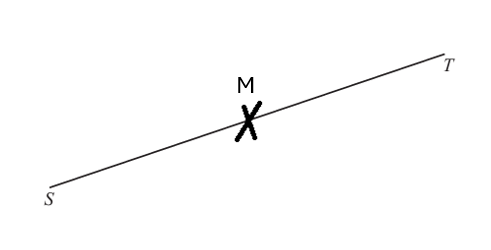
Mark the midpoint of the line ST.

To mark the midpoint of the line segment ST:

1. Identify Points S and T: Locate points S and T on the line.
2. Find the Midpoint: The midpoint of a line segment is the point that divides the segment into two equal parts. With a ruler, you can measure the length of ST and find the halfway point.
3. Label the Midpoint: Once you have located the midpoint, mark it with a point and label it, often with a letter such as M.

0580/12/02/03/24/07

The range of eight numbers is 31.
These are seven of the numbers.

$$28364224381621$$

Find the two possible values of the eighth number.

Range of the eight numbers: 31
Seven numbers: 28, 36, 42, 24, 38, 16, 21

Determine the current range

First, find the minimum and maximum values among the seven numbers given:

Minimum value = 16
Maximum value = 42

Calculate the possible range with the eighth number

Since the range of all eight numbers is 31, we need to find the smallest and largest possible values for the eighth number to achieve this range.

If the eighth number is the new maximum:

$$Range=Newmaximum-16=31$$

$$Newmaximum=31+16=47$$

So, one possible value for the eighth number is 47.

If the eighth number is the new minimum:

$$Range=42-Newminimum=31$$

$$Newminimum=42-31=11$$

So, another possible value for the eighth number is 11.

Answer is 11 or 47

0580/12/02/03/24/09

Simplify $4m+7k-m+3k$

Group like terms

Group the terms with m: $4m–m$
Group the terms with k: $7k+3k$

Simplify each group

Simplify the m-terms: $4m–m=3m$
Simplify the k-terms: $7k+3k=10k$

Write the simplified expression

Now combine the simplified terms: $3m+10k$

Answer is 3m + 10k